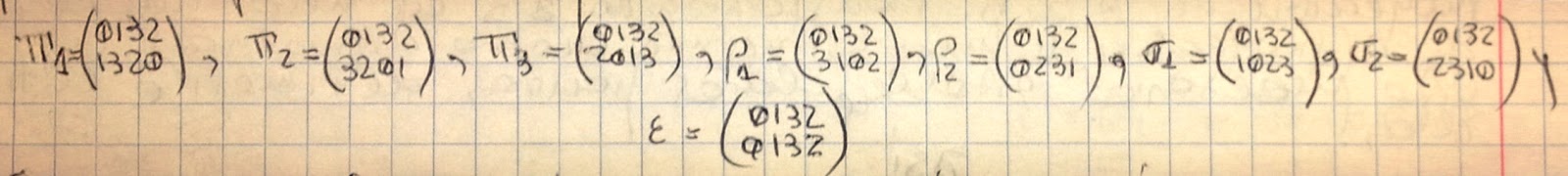Historia de la Lógica Transcursiva (Capítulo 243)
Cuaderno XI (páginas 1459 a 1464)
(Hoy veremos la relación que tiene el Código Genético (CG) con los números binarios. Un adelanto de la introducción del segundo capítulo de la Tesis; y algunos precursores de mi sistema lógico, entre ellos, Galois, el 'inventor' de los grupos.)
(Tomamos como referencia el trabajo de R. Sanchez; E. Morgado; R. Grau, "The Genetic Code Boolean Lattice" - 'El código genético como una matriz booleana' - Commun. Math. Comput. Chem. 52, pp. 29-46, 2004)
Las estructuras algebraicas del CG son muy importantes para obtener información sobre el significado del código y sus aplicaciones. Los autores definen dos matrices booleanas duales de codones, del CG, usando el número de uniones o puentes de hidrógeno, y el tipo químico de las bases: purinas y pirimidinas. [aclaramos que mi codificación binaria de las bases no es algo original, anteriormente, otros investigadores hicieron propuestas similares, aunque yo las desconocía. Vamos a analizar rápidamente, todas las que encontré a posteriori. Jiménez-Montaño et al. (1996) sugieren la siguiente correspondencia: A = 00, G = 01, U = 10, C = 11. Este código binario de seis variables pueden ser representadas por un hipercubo booleano; no coincide con el nuestro. Karasev y Stefanov (2001) sugieren la siguiente correspondencia: C = 00, U = 01, G = 10, A = 11; que tampoco coincide con lo nuestro. He et al (2004) usando el código Gray (una variante de código binario) proponen lo siguiente: C = 00, U = 10, G = 11, A = 01; distinta a nuestra propuesta. Finalmente, Stambuk (2000) introduce las propiedades métricas universales del código genético, definidas mediante la representación de las bases en un cuadrado cuyas vértices son U o T = 00, C = 01, G = 10 y A = 11 que, si bien es exactamente igual a nuestra codificación, la asignación se hace de acuerdo a criterios levemente distintos. Este autor le asigna el primer dígito del código a la característica química primaria: 0 a las pirimidinas y 1 a las purinas; mientras que el segundo dígito se lo asigna a la característica química secundaria: 0 a las bases que poseen en su molécula un grupo cetona, y un 1 a las que poseen un grupo amino. ¡Muy lógica la asignación; inclusive, mejor que la mía!]
Las matrices booleanas reflejan el rol de la hidrofobicidad en la distribución de la asignación de un codón a cada aminoácido (aa). Particularmente, las imágenes simétricas de los codones con la base A(denina) en segundo lugar, codificando los aa hidrofílicos; y son siempre codones con la base U(racilo) en el segundo lugar, los que codifican los aa hidrofóbicos, tal como se los representa en los diagramas de Hasse.
Los aa con C(itosina) en el segundo lugar tienen una polaridad intermedia entre los otros dos, y los aa con G(uanina) en el segundo lugar, no tienen ninguna regularidad en su polaridad. Podríamos decir que los aa hidrófilos se pueden representar por 01, los hidrófobos por 10, luego los intermedios serán 11, y los sin polaridad 00. Según lo anterior, entonces, los aa hidrófilos tienen 01⊕10 = 11 (A en segundo lugar). Los aa hidrófobos tienen 01≣10 = 00 (U en segundo lugar). Los intermedios (11) tienen 11⊕10 = 01 (C en segundo lugar); mientras que, los que carecen de polaridad (00) tienen 00≣01 = 10 (G en segundo lugar). {¡No está mal!}
Se ha destacado la organización no aleatoria del CG; y varias hipótesis han sido propuestas para explicar su enigmático orden, cuyo origen permanece desconocido. {se le olvida que la tabla que se utiliza para trabajar es producto de una convención. [se queremos ser consecuentes con nuestra teoría, podríamos agregar que el origen de este 'maravilloso orden' está en el lenguaje universal que da fundamento a todo lo real]} Con este propósito se han desarrollado distintos modelos matemáticos, para explicar la representación binaria de las bases del ADN.
El CG es el sistema bioquímico para la expresión del gen. Tiene que ver con la traslación o descodificación de la información contenida en la estructura primaria del ADN y ARN, dentro de la secuencia proteica. Por tanto, el CG es, a la vez, un sistema físico-químico y un sistema de comunicación. Físicamente, el reconocimiento molecular depende del grado de complementariedad entre las superficies moleculares interactuantes, por medio de una unión laxa; informacionalmente, un prerrequisito para definir un código, es el concepto de distinción. - En cuanto al aspecto comunicacional, no aporta absolutamente nada.
────────────────────────────────────────────
Borrador de la introducción general y del segundo capítulo:
La hipótesis central es: la estructura y simetría natural (la de la doble espiral del ADN), patrimonio de todos los seres vivos, es compartida por todos los sistemas reales. En otros términos, las leyes que rigen a estas moléculas auto-organizadas, desde un periodo de tiempo indefinido, nos dan la pauta organizativa de todos los aspectos de la realidad, aquí considerados, convirtiéndose por tanto, en universales.
Nuestra comprensión de esta maravilla natural, que representa el método por medio del cual la vida permanece en el tiempo, generando más vida, se basa en lo que ha llamado 'código genético'. Esta metáfora que pretende representar el proceso responsable de la síntesis proteica (una de las bases de la vida), es producto de una convención. Esta tabla de tres entradas nos pinta un panorama abstracto, simplista y unidimensional de la relación de 'contigüidad' de tres nucleótidos (o bases), tomados de los cuatro existentes, pero sin tener en cuenta el contexto en donde se supone que estos codones (como se llama al grupo de tres nucleótidos), operan. Dicho de otra forma, la fuerte creencia actual de que los codones significan 'literalmente' aminoácidos, y que una secuencia de estos aminoácidos, significan literalmente proteínas, como bien puntualiza White (2007), no es un modelo lógico aceptable.
Como nuestro propósito es demostrar que la organización lógica de la base de la vida es, en definitiva, la lógica que 'ordena' toda la realidad, es imprescindible elaborar una estrategia de análisis de lo hoy disponible, para despejar las notorias semejanzas existentes entre lo vivo, lo psíquico y lo socio-cultural.
Para llevar a cabo nuestra tarea, replantearemos, en sus rasgos básicos, la organización de la 'tabla de codones', para que pueda interpretarse como un 'mapa' que nos indique como estos codones pueden traducirse en aminoácidos, y luego estos, en proteínas, y poder, en capítulos posteriores, plasmar esa sucesión lógica, en los demás sistemas reales.
Podemos ver, fácilmente, esta reorganización, si la asimilamos al concepto de función (visto en el capítulo anterior). La clase A, aquí son los codones, y la clase B los aminoácidos, y entre ellas existe una fuerte relación estructural (lógica). Hay una proyección de A hacia B, transformando a B, en una 'imagen' de A (proyección de una estructura en otra estructura; y esto, necesariamente, establece claras pautas de simetría entre ellas.
────────────────────────────────────────────
Los Precursores: Evariste Galois - Camille Jordan:
El aporte más importante de Galois es sobre la resolutividad de las ecuaciones algebraicas en radicales. Aunque, más que sus teoremas probados, es el método utilizado, lo más importante. O sea, no qué probó, sino cómo lo hizo, es lo realmente importante para mi trabajo.
Galois basa su trabajo en ciertas apreciaciones sobre el 'grado de simetría' de una ecuación algebraica.
Evidentemente, la ecuación de quinto grado:
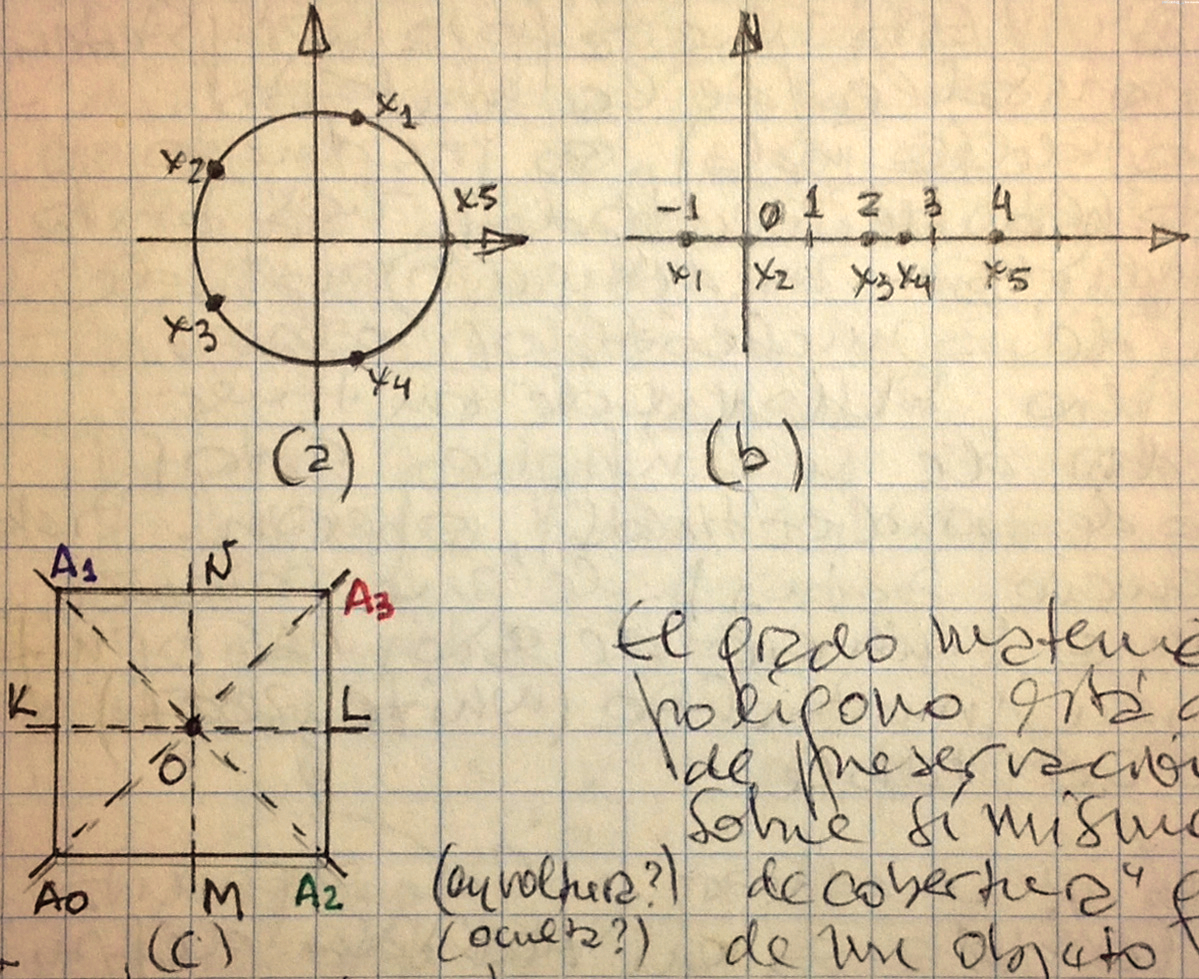
x⁵ - 1 = 0; (a) → muestra sus raíces complejas, es más simétrica que la ecuación:
x⁵ - x⁴ + x³ + x² + 2 = 0; y que la ecuación:
2x⁵ - 15x⁴ + 29x³ - 6x² - 40x = 0, cuyas raíces son x1 = -1; x2 = 0; x3 = 2; x4 = 2½; x5 = 4, como lo muestra (b).
El grado matemático de simetría de un polígono está dado por el conjunto de mapas de preservación de distancias del polígono, sobre sí mismo. Esto da la idea de una 'operación de cobertura', que es una transformación geométrica de un objeto que lo deja sin cambios aparentes.
Para el cuadrado (c) de la figura, de vértices A0, A1, A3, A2, este conjunto incluye la rotación de 90º alrededor de su centro O, lo cual envía los vértices A0, A1, A3, A2 → A1, A3, A2, A0. Esta rotación también puede ser expresada por la permutación (0132→1320), lo que nos indica que el vértice 0 ha sido enviado al vértice 1, el 1 al 3, y así sucesivamente. La rotación (0132→3201) es de 180º (o reflexión en O). La rotación (0132→2013) es de 270º. Las reflexiones (0132→3102) y (0132→0231) se realizan sobre las diagonales A1A2 y A3A0, respectivamente; y las reflexiones (0132→1023) y (0132→2310), sobre las líneas medias: KL y NM, respectivamente.
Por supuesto, la transformación de identidad (0132→0132), no mueve ningún vértice. {en realidad dieron una vuelta completa en cualquiera de los ejes} En resumen: el conjunto de transformaciones de un cuadrado, sobre sí mismo, está dado por las 8 permutaciones siguientes:
[continuará ... ]
¡Nos vemos mañana!
(Hoy veremos la relación que tiene el Código Genético (CG) con los números binarios. Un adelanto de la introducción del segundo capítulo de la Tesis; y algunos precursores de mi sistema lógico, entre ellos, Galois, el 'inventor' de los grupos.)
(Tomamos como referencia el trabajo de R. Sanchez; E. Morgado; R. Grau, "The Genetic Code Boolean Lattice" - 'El código genético como una matriz booleana' - Commun. Math. Comput. Chem. 52, pp. 29-46, 2004)
Las estructuras algebraicas del CG son muy importantes para obtener información sobre el significado del código y sus aplicaciones. Los autores definen dos matrices booleanas duales de codones, del CG, usando el número de uniones o puentes de hidrógeno, y el tipo químico de las bases: purinas y pirimidinas. [aclaramos que mi codificación binaria de las bases no es algo original, anteriormente, otros investigadores hicieron propuestas similares, aunque yo las desconocía. Vamos a analizar rápidamente, todas las que encontré a posteriori. Jiménez-Montaño et al. (1996) sugieren la siguiente correspondencia: A = 00, G = 01, U = 10, C = 11. Este código binario de seis variables pueden ser representadas por un hipercubo booleano; no coincide con el nuestro. Karasev y Stefanov (2001) sugieren la siguiente correspondencia: C = 00, U = 01, G = 10, A = 11; que tampoco coincide con lo nuestro. He et al (2004) usando el código Gray (una variante de código binario) proponen lo siguiente: C = 00, U = 10, G = 11, A = 01; distinta a nuestra propuesta. Finalmente, Stambuk (2000) introduce las propiedades métricas universales del código genético, definidas mediante la representación de las bases en un cuadrado cuyas vértices son U o T = 00, C = 01, G = 10 y A = 11 que, si bien es exactamente igual a nuestra codificación, la asignación se hace de acuerdo a criterios levemente distintos. Este autor le asigna el primer dígito del código a la característica química primaria: 0 a las pirimidinas y 1 a las purinas; mientras que el segundo dígito se lo asigna a la característica química secundaria: 0 a las bases que poseen en su molécula un grupo cetona, y un 1 a las que poseen un grupo amino. ¡Muy lógica la asignación; inclusive, mejor que la mía!]
Las matrices booleanas reflejan el rol de la hidrofobicidad en la distribución de la asignación de un codón a cada aminoácido (aa). Particularmente, las imágenes simétricas de los codones con la base A(denina) en segundo lugar, codificando los aa hidrofílicos; y son siempre codones con la base U(racilo) en el segundo lugar, los que codifican los aa hidrofóbicos, tal como se los representa en los diagramas de Hasse.
Los aa con C(itosina) en el segundo lugar tienen una polaridad intermedia entre los otros dos, y los aa con G(uanina) en el segundo lugar, no tienen ninguna regularidad en su polaridad. Podríamos decir que los aa hidrófilos se pueden representar por 01, los hidrófobos por 10, luego los intermedios serán 11, y los sin polaridad 00. Según lo anterior, entonces, los aa hidrófilos tienen 01⊕10 = 11 (A en segundo lugar). Los aa hidrófobos tienen 01≣10 = 00 (U en segundo lugar). Los intermedios (11) tienen 11⊕10 = 01 (C en segundo lugar); mientras que, los que carecen de polaridad (00) tienen 00≣01 = 10 (G en segundo lugar). {¡No está mal!}
Se ha destacado la organización no aleatoria del CG; y varias hipótesis han sido propuestas para explicar su enigmático orden, cuyo origen permanece desconocido. {se le olvida que la tabla que se utiliza para trabajar es producto de una convención. [se queremos ser consecuentes con nuestra teoría, podríamos agregar que el origen de este 'maravilloso orden' está en el lenguaje universal que da fundamento a todo lo real]} Con este propósito se han desarrollado distintos modelos matemáticos, para explicar la representación binaria de las bases del ADN.
El CG es el sistema bioquímico para la expresión del gen. Tiene que ver con la traslación o descodificación de la información contenida en la estructura primaria del ADN y ARN, dentro de la secuencia proteica. Por tanto, el CG es, a la vez, un sistema físico-químico y un sistema de comunicación. Físicamente, el reconocimiento molecular depende del grado de complementariedad entre las superficies moleculares interactuantes, por medio de una unión laxa; informacionalmente, un prerrequisito para definir un código, es el concepto de distinción. - En cuanto al aspecto comunicacional, no aporta absolutamente nada.
────────────────────────────────────────────
Borrador de la introducción general y del segundo capítulo:
La hipótesis central es: la estructura y simetría natural (la de la doble espiral del ADN), patrimonio de todos los seres vivos, es compartida por todos los sistemas reales. En otros términos, las leyes que rigen a estas moléculas auto-organizadas, desde un periodo de tiempo indefinido, nos dan la pauta organizativa de todos los aspectos de la realidad, aquí considerados, convirtiéndose por tanto, en universales.
Nuestra comprensión de esta maravilla natural, que representa el método por medio del cual la vida permanece en el tiempo, generando más vida, se basa en lo que ha llamado 'código genético'. Esta metáfora que pretende representar el proceso responsable de la síntesis proteica (una de las bases de la vida), es producto de una convención. Esta tabla de tres entradas nos pinta un panorama abstracto, simplista y unidimensional de la relación de 'contigüidad' de tres nucleótidos (o bases), tomados de los cuatro existentes, pero sin tener en cuenta el contexto en donde se supone que estos codones (como se llama al grupo de tres nucleótidos), operan. Dicho de otra forma, la fuerte creencia actual de que los codones significan 'literalmente' aminoácidos, y que una secuencia de estos aminoácidos, significan literalmente proteínas, como bien puntualiza White (2007), no es un modelo lógico aceptable.
Como nuestro propósito es demostrar que la organización lógica de la base de la vida es, en definitiva, la lógica que 'ordena' toda la realidad, es imprescindible elaborar una estrategia de análisis de lo hoy disponible, para despejar las notorias semejanzas existentes entre lo vivo, lo psíquico y lo socio-cultural.
Para llevar a cabo nuestra tarea, replantearemos, en sus rasgos básicos, la organización de la 'tabla de codones', para que pueda interpretarse como un 'mapa' que nos indique como estos codones pueden traducirse en aminoácidos, y luego estos, en proteínas, y poder, en capítulos posteriores, plasmar esa sucesión lógica, en los demás sistemas reales.
Podemos ver, fácilmente, esta reorganización, si la asimilamos al concepto de función (visto en el capítulo anterior). La clase A, aquí son los codones, y la clase B los aminoácidos, y entre ellas existe una fuerte relación estructural (lógica). Hay una proyección de A hacia B, transformando a B, en una 'imagen' de A (proyección de una estructura en otra estructura; y esto, necesariamente, establece claras pautas de simetría entre ellas.
────────────────────────────────────────────
Los Precursores: Evariste Galois - Camille Jordan:
El aporte más importante de Galois es sobre la resolutividad de las ecuaciones algebraicas en radicales. Aunque, más que sus teoremas probados, es el método utilizado, lo más importante. O sea, no qué probó, sino cómo lo hizo, es lo realmente importante para mi trabajo.
Galois basa su trabajo en ciertas apreciaciones sobre el 'grado de simetría' de una ecuación algebraica.
Evidentemente, la ecuación de quinto grado:
x⁵ - 1 = 0; (a) → muestra sus raíces complejas, es más simétrica que la ecuación:
x⁵ - x⁴ + x³ + x² + 2 = 0; y que la ecuación:
2x⁵ - 15x⁴ + 29x³ - 6x² - 40x = 0, cuyas raíces son x1 = -1; x2 = 0; x3 = 2; x4 = 2½; x5 = 4, como lo muestra (b).
El grado matemático de simetría de un polígono está dado por el conjunto de mapas de preservación de distancias del polígono, sobre sí mismo. Esto da la idea de una 'operación de cobertura', que es una transformación geométrica de un objeto que lo deja sin cambios aparentes.
Para el cuadrado (c) de la figura, de vértices A0, A1, A3, A2, este conjunto incluye la rotación de 90º alrededor de su centro O, lo cual envía los vértices A0, A1, A3, A2 → A1, A3, A2, A0. Esta rotación también puede ser expresada por la permutación (0132→1320), lo que nos indica que el vértice 0 ha sido enviado al vértice 1, el 1 al 3, y así sucesivamente. La rotación (0132→3201) es de 180º (o reflexión en O). La rotación (0132→2013) es de 270º. Las reflexiones (0132→3102) y (0132→0231) se realizan sobre las diagonales A1A2 y A3A0, respectivamente; y las reflexiones (0132→1023) y (0132→2310), sobre las líneas medias: KL y NM, respectivamente.
Por supuesto, la transformación de identidad (0132→0132), no mueve ningún vértice. {en realidad dieron una vuelta completa en cualquiera de los ejes} En resumen: el conjunto de transformaciones de un cuadrado, sobre sí mismo, está dado por las 8 permutaciones siguientes:
[continuará ... ]
¡Nos vemos mañana!