Aprend3r / Portal Educativo

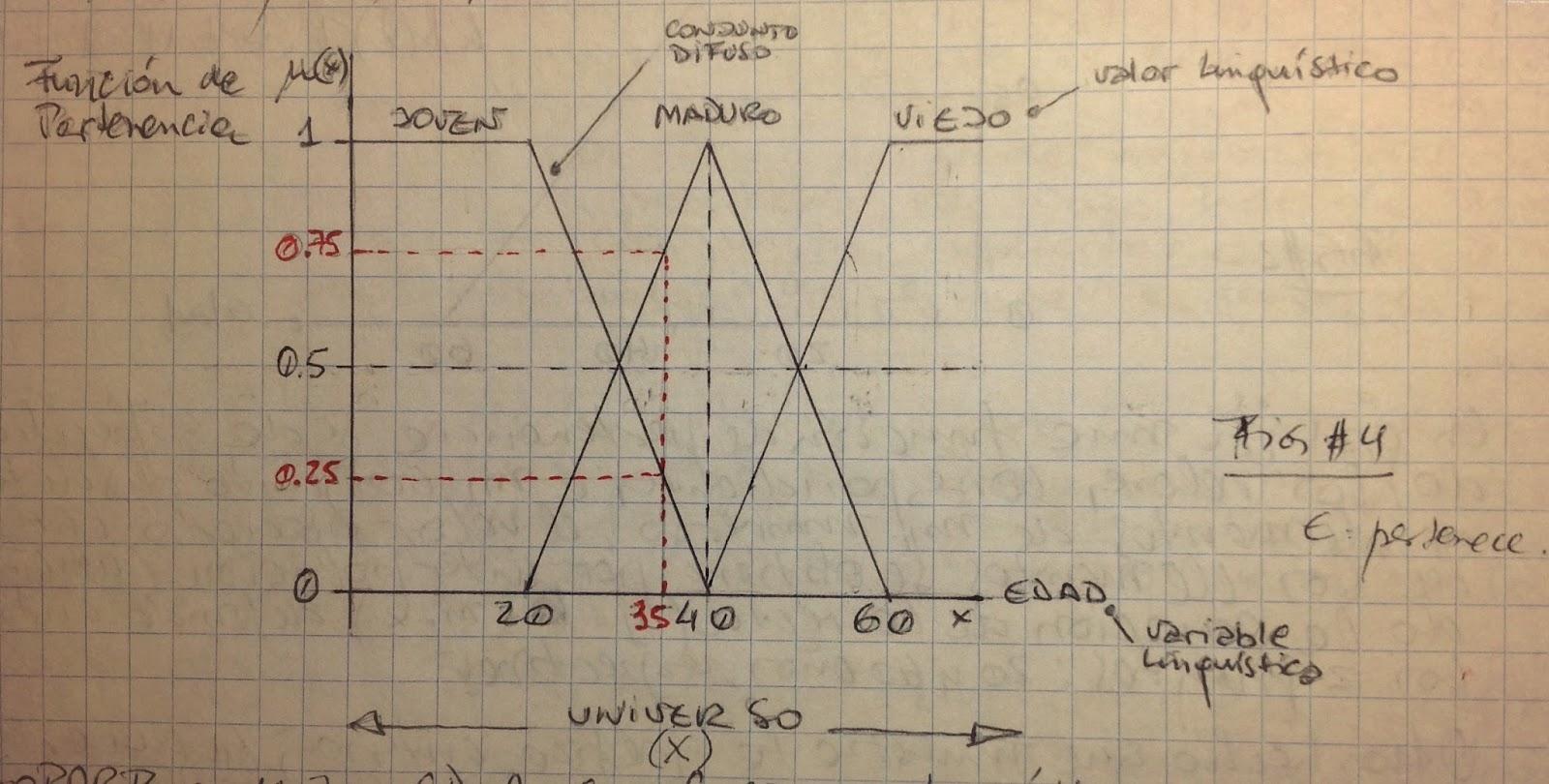
Cuaderno VII (páginas 831 a 836) (Continuamos con el trabajo de Lakoff) Cap. 17 - Semántica Cognitiva: Fundamentos: Los estudios empíricos realizados por Berlin, Rosch, y otros han arrojado evidencias de un nivel significativo de interacción humana con el entorno (el nivel básico), caracterizado por la conducta perceptiva, imaginería mental y movimientos motores. A este nivel, las personas funcionan más eficiente y exitosamente en relación con discontinuidades del entorno natural. Es a este nivel de la experiencia física que nosotros podemos distinguir adecuadamente tigres de elefantes, sillas de mesas, etc. Un nivel más abajo, las cosas son más difíciles. Es mucho más difícil distinguir una especie de jirafa de otra, que una jirafa de un elefante. Nuestra capacidad de conducta perceptiva de 'nivel básico' no hacen fácil las determinaciones a estos bajos niveles. [ un marcado nivel de vaguedad en las definiciones; una característica que define toda la obra de Lakoff ] ...

Cuaderno VII (páginas 825 a 830) (Hoy comenzamos un nuevo cuaderno (06/2005) en donde hacen su aparición los trabajos de una figura relevante en la base lógica de la Teoría final: Gotthard Günther (1900-1984): filósofo alemán, cuya obra está basada en los trabajos de Hegel, Heidegger y Spengler. El invento de la 'lógica transclásica' fue el intento de combinar los resultados mejorados de la dialéctica moderna con la lógica formal. Sus estudios sobre el problema filosófico del 'Du' ('Tú') abrió un nuevo camino en el campo del análisis de la subjetividad. Sus principales obras: Fundamentos de una nueva teoría del pensamiento en la lógica de Hegel (1933) - Idea y esbozo de una lógica no aristotélica (1959) - Aportaciones a los cimientos de una dialéctica operativa (Vol.1 (1976), Vol.2 (1979), Vol.3 (1980)) (Iniciamos el análisis de " Women, fire and dangerous things " (Mujeres, fuego y cosas peligrosas) de George Lakoff - 1987, como una iniciación ...

Cuaderno VI (páginas 819 a 824) Enfoque diádico de la realidad (los ensambles): Es preciso aclarar que este enfoque no está emparentado con el concepto filosófico de dualismo, o sea, con la interpretación del mundo desde el punto de vista cartesiano: división irreversible entre cuerpo y alma. Una diada o relación diádica, en este caso, es tomada como la expresión compleja (Morin) que relaciona dos elementos que en todos los casos son: opuestos (antagónicos), complementarios y concurrentes (simultáneos). A esta dianas le damos el nombre de: 'ensambles', y con ello se pretende caracterizar compuestos en donde sus elementos constitutivos se interrelacionan animados por una 'trilógica': lógica binaria (bivalente), lógica difusa (multivalente), y lógica relacional (o isomérica) Lo que puede ser tildado de real obedece a este esquema básico, a este patrón organizacional que hace compatibles dinámicamente las distintas estructuras reales a través de sus funciones respe...

Cuaderno VI (páginas 813 a 818) No se puede dejar de ver que la estructuración sintáctica de la realidad es capaz de expresar solo las relaciones de los 'objetos' reales (o sea, su organización), y caracterizar el tiempo externo, el que sirve para datar. Pero está faltando un aspecto que está en la constitución del PAU y que hace que sea un verdadero sistema: su capacidad de reorganizarse, y esto por supuesto, está en la 'sintaxis psíquica' y por lo tanto, se refleja en la sintaxis del lenguaje. Entonces, el lenguaje puede expresar el tiempo interno (pasado, presente, futuro) en relación con el externo y enmarcar en una expresión, no solo en forma automática, la relación de elementos léxicos básicos, sino una estructura argumental asociada a una acción, al incluir ésta (verbo) en su interrelación discreto/continuo (tiempo de la datación/tiempo del recuerdo, del ahora y el de la proyección). Esta capacidad de reconocer la estructura argumental tiene su base en cómo est...

Cuaderno VI (páginas 807 a 812) Algunas ideas sobre el lenguaje (origen): Si tomamos lenguaje en el sentido lato y aún en el sentido que lo exigen los lingüistas, o sea: que es algo que debe tener sintaxis, podemos asegurar que el lenguaje no es patrimonio del hombre. El lenguaje es inherente a la condición de vida que tiene una función evidente: la comunicación; pero esta no es su única ni primordial función, sino la de posibilitar la supervivencia. Lenguaje es vida. Lenguaje es sintaxis funcionalidad, entendiendo como sintaxis una estructura relacional entre objetos. La sintaxis del lenguaje así definido, surge de la realidad. La realidad tiene tres ejes que la enmarcan: estructural, dinámico y funcional {según ya lo hemos visto}, con un nivel de complejidad creciente. Se postula un compromiso entre los ejes de la realidad y la estructura proto-psíquica/Psíquica de los seres vivos, el cual da sustento a la sintaxis del nivel de lenguaje que dispone cada especie (entendiendo e...

Cuaderno VI (páginas 801 a 806) Algunas ideas sobre la psiquis: Dijimos que los seres unicelulares y cada una de nuestras células entre ellos, poseen una proto-psiquis, y que era asimilada a su condición de vida (¿procesos autopoiéticos?), y en donde, quien ejerce la función de control y mantiene la vida de relación con el entorno y con otras semejantes es la membrana celular en los procariotas, y junto con el núcleo en los eucariotas. En los multicelulares se hace necesario la aparición de un nuevo tipo de célula que, fuera de controlarse a sí misma, sude a coordinar el funcionamiento de todas las células en conjunto, como un todo organizado que debe adaptarse y sobrevivir como tal. Estas células son las células nerviosas que facultan una potenciación de los mecanismos físico-químicos que sostienen la vida de esta 'comunidad' celular, representando el factor decisivo para que este conglomerado celular está 'vivo'. Aquí ya existe una verdadera proto-psiquis, en el...

Cuaderno VI (páginas 795 a 800) (Continuamos con el abordaje de la realidad que hace la Lógica Difusa) - Variables lingüísticas: son aquellos conceptos o nociones que se califica de forma difusa, para dar cuenta de su carácter continuo (altura, edad, nivel emocional, etc.). Se denominan 'lingüísticos' porque se definen mediante términos del lenguaje común. -Valor lingüístico: los distintas calificaciones que efectúan sobre la variable lingüística: muy joven, algo joven, poco joven, no joven, etc. (joven, maduro, viejo). Al conjunto difuso (CD) ahora lo podemos definir como un valor lingüístico junto a una función de pertenencia. El valor es el 'nombre' del conjunto y la función de pertenencia es aquella aplicación que asocia a cada elemento del universo, el grado con que pertenece al CD, indicando su relación con cada valor lingüístico. Se dice que un conjunto es 'nítido' si su función de pertenencia toma valores {0,1} y 'difuso' si toma valo...

Cuaderno VI (páginas 789 a 794) (Continuamos con el análisis de los aportes de la lógica difusa al estudio de la realidad) A pesar de la pertinencia de la lógica difusa para lidiar con sistemas reales, se debe aclarar que esto es solo aparente, pues no existe una teoría de conjuntos difusos que haga equivaler esos conjuntos con los 'objetos reales'. Los conjuntos difusos son siempre (y solamente) 'funciones', sobre un 'universo de objetos', dentro de un rango de pertenencia a ese universo entre 0 y 1. En otras palabras, las funciones que rastrean un determinado objeto dentro del intervalo unidad, pueden ser conjuntos difusos, pero llegan a serlo cuando, y solo cuando, coinciden con alguna descripción semántica, intuitivamente plausible, de alguna propiedad imprecisa de los objetos de ese intervalo. Veamos lo anterior con un ejemplo: definir los números reales en el intervalo entre 20-60 es un problema que tiene implícitos, límites francos, y por lo tanto, ...

Cuaderno VI (páginas 783 a 788) (Continuamos con las propuestas generales del trabajo) La Cibernética clásica, la Teoría de Sistemas y aún la Lógica tradicional, tratan de descubrir las categorías de elementos reales funcionando como parte de una organización, vale decir, estructuras relacionales (sistemas) sobre los que se ejerce y los que ejercen alguna actividad de control. Desde este punto de vista se pretende descubrir cómo funciona la realidad. Aceptando como actores necesarios de la realidad: el sujeto (S), el objeto (O), y el cambio (V) que conecta a los dos anteriores, la perspectiva tradicional los relaciona de la siguiente forma: (figura) Esta relación de elementos representa una 'máquina trivial' (von Foerster) que enlaza elementos concretos (discretos), categorías absolutas de una manera inerte (sin vida), ya que, aunque la pretendida acción (V) de control se ejerza en forma reflexiva (feedback ⊖   o   ⊕), también se hace en forma exclusivamente discreta...