Historia de la Lógica Transcursiva (Capítulo 259)
Cuaderno XI (páginas 1555 a 1560)
(El 23/7/2008 se publica en Aprend3r la segunda parte de "Ficciones", y es lo que hoy veremos en este capítulo)
En esta segunda parte intentaremos caracterizar una observación semiótica de la realidad, considerando la Semiótica como la lógica del sentido (según ya vimos). El hecho de basarse en la observación como método de análisis es adecuado, ya que de esta forma se evita la ‘presunción imperialista’ (como dice Eco) de suponer que la Semiótica puede explicarlo todo. Todo puede ser tratado semióticamente, que es algo muy distinto.
Para comenzar debemos establecer parámetros concretos, reales y tangibles para poder así procurar una definición (aproximarse al límite aristotélico) de algunos conceptos que por ser tales, carecen (en apariencia ) de realidad. Uno, entre otros, que necesita imperiosamente de un límite es el concepto de infinito (qué paradójico, ¿No?).
Hemos dicho que no hay nada infinito. Esto, a primera vista, es cierto si nos referimos a la apariencia que nos ofrecen los cuerpos materiales; pero, no lo es tanto si pretendemos justificar otras cosas. Entonces nos percatamos que pueden definirse, al menos, tres infinitos: a) Un infinito por suma, que es el concepto de Número; b) Un infinito por división, que es el concepto de Espacio; y c) Un infinito en ambos sentidos, que es el concepto de Tiempo. Luego, tendría sentido presuponer una infinitud corpórea que ha de entenderse como lo contrario a evidente, superficial y discreto. Este es un infinito que se alcanzaría paulatinamente, en forma oculta, en ‘las profundidades’ de la realidad, y, que surgiría explosivamente a la apariencia (se manifestaría como ‘verdad’) en un ir haciéndose; en un alcanzar el límite; en un provocar catástrofes; en un producir bifurcaciones; en una palabra, en un definirse. Esta definición lo es a modo de una perturbación variable (cambio) aunque con cierta estabilidad que en cada instante del tiempo irreversible tiene dimensiones finitas, a pesar de manifestarse por un Número y ocupar un Espacio en un Tiempo determinado, que no lo son.
Habiendo de alguna manera, ‘corporeizado’ el infinito, retomamos la Babel borgeana, en la que, más allá de los múltiples acertijos (de los que haremos caso omiso) hay un fuerte planteo paradojal, dialéctico (en el sentido hegeliano; o mejor heracliteano) y según trataremos de demostrar, real.
Ya desde Einstein quedó claramente establecido (muy a pesar de Newton), que toda simultaneidad es relativa. Esta relatividad tiene que ver con el simple hecho de estar obligados a elegir un sistema de referencia particular (no olvidar que en ciencia trabajamos con convenciones). Borges nos plantea algo distinto al absoluto newtoniano y al relativismo de Einstein; aproximándose a los presocráticos, nos pinta un universo cual pergeño alucinante de un devenir perpetuo de polos opuestos simultáneos que en su cíclico cambio, siempre termina (para comenzar) siendo lo mismo.
Todo esto suena a ilógico, a meros términos ‘sin sentido’, a un ruido de fondo que intenta tapar la evidencia; a un protocolo aventurado que nunca conseguirá ponerse a la altura de las circunstancias formales y por más que de ‘vueltas’, nunca será más que un delirante paralogismo. Si lo vemos con los ojos de la lógica clásica, sí. Si corregimos nuestra miopía con la óptica de una de las tantas lógicas alternativas posibles, no.
Imaginemos solo por un instante, que nos hemos propuesto descifrar la estructura de la realidad (¡Menuda tarea!)
Si hablamos de estructura, hablamos de relaciones; y si hablamos de relaciones, estamos diciendo algo sobre elementos que se relacionan; y si hablamos de elementos, estamos resaltando diferencias y además la simultaneidad en la aprehensión de al menos dos elementos distintos.
La concurrencia de la aprehensión de dos elementos exige, por un lado, que ambos tengan algo en común y por otro, que haya algo que los diferencie. Veamos esto último a través de un ejemplo simple: supongamos que tenemos ante nosotros dos pelotas, y que una de ellas es rayada y la otra lisa. Estos elementos están relacionados de dos maneras en forma simultánea: tienen algo en común que los identifica como pelota (p.e. la forma) y algo que los diferencia como elementos distintos pertenecientes a una categoría determinada, el hecho de ser una rayada, y la otra no.
La tabla I muestra una manera (entre otras) de representar ‘numéricamente’ ambas pelotas (que ya es ‘rozar’ uno de los infinitos). Este método se basa en dejar constancia de las oposiciones que caracterizan los elementos; o sea, de aquello que permite distinguirlos (presencia o ausencia de un atributo dado).
Se puede observar que la cifra que representa cada elemento, tiene dos lugares, entonces, la mitad no ocupada (representada por el 0), se la asignaremos a aquel atributo que hace que los dos elementos pertenezcan a la misma categoría (la forma); es decir, para consignar que ambos son pelotas. Esta simple estructura se puede representar como lo muestra la (figura 1).
Desde el punto de vista lógico podemos ver, en la Figura 1, que ambos elementos guardan una doble relación: i) son opuestos; es decir, uno es la negación del otro (negar 01 es reemplazarlo por su inverso 10, y viceversa), y ii) son complementarios porque uno tiene una característica de la que el otro carece. Pero además este esquema nos muestra otros aspectos relacionales que subyacen a la aprehensión de ambos elementos. Así, por un lado tenemos la conjunción por aquel aspecto o atributo que tienen en común (la forma), y por otro la disyunción por aquel atributo que los diferencia (textura).
La conjunción como operación lógica nos dice que una relación será verdadera (y asumirá un valor 1) cuando ambos elementos de la relación sean verdaderos (evidentes), de lo contrario será falsa (asumirá un valor 0); por eso 01∩10 = 00. En cuanto a la disyunción nos dice que será falsa (0) únicamente cuando ambos elementos disyuntivos sean falsos, de lo contrario será verdadera (1); entonces 01∪10 = 11.
De acuerdo a lo anterior estamos autorizados para decir, según la lógica de clases, que 11 representa la unión de aquellos aspectos que distinguen un elemento de otro, y que 00 representa la separación (intersección) de aquel aspecto que los reúne (categoría). Es importante notar además, que 11 y 00 guardan entre sí la misma doble relación de oposición y complementariedad. Por tanto, y siguiendo en la lógica de clases, podemos afirmar que en este pequeño universo que hemos caracterizado, hay dos clases o conjuntos: la de los elementos (con su ámbito (01) y su complemento (10)), y la del cambio o transformación (con su ámbito (11) y su complemento (00)) que surge cuando dos objetos se relacionan entre sí.
Cuando analizamos otras oposiciones relacionadas con los mismos objetos, descubrimos algo interesante. Por ejemplo, pelota grande vs. pelota pequeña. Esta última oposición ya no es binaria (no tiene solo dos términos: el elemento y su opuesto), sino que al menos, admite un término intermedio como lo es pelota mediana. En realidad este tipo de atributos, acepta infinitos valores entre sus extremos. De esta manera, si pretendemos ‘describir’ lo que ocurre en la realidad de este nuestro limitado universo, debemos poder caracterizar todas las posibilidades. Una forma de hacerlo es ampliar el esquema anterior, profundizando en su estructura y mostrar así, que en definitiva, todo se restringe a un interjuego entre el ‘ser’ y el ‘parecer’. El ‘parecer’, aquello que se ofrece en directo a la aprehensión y que tildaremos de ‘superficial’, es de tipo binario o discreto; se pasa de un extremo al otro de la comparación sin valores intermedios, siendo así un atributo absoluto y evidente. El ‘ser’ en cambio, es aquello que ‘no se ve’, que permanece oculto y por lo que lo llamamos profundo y admite infinitos valores intermedios entre sus extremos; esta última característica lo convierte en un atributo continuo o analógico y relativo pues resulta su valoración, de una comparación (de un marco de referencia).
Hipotéticamente y de una forma genérica, se puede utilizar como base de la observación semiótica la relación sujeto/objeto. Aquí sujeto (S) es considerado como la ‘fuente’ del cambio y el objeto (O) como el ‘destino’ de ese cambio, y ambos están relacionados precisamente por tal cambio que queda expresado por una operación de disyunción (cambio aparente = V) en la superficie y por una operación de conjunción (cambio oculto = ⊽) en lo profundo. (figura 2)
Los vértices del ‘cuadrado’ propuesto (figura 2) representan lo que llamamos: nichos o lugares ontológicos, que serán ocupados por elementos de sentido (contenidos) concretos (el segundo infinito); contenidos que, en la elaboración de la dinámica, no son tenidos en cuenta.
Si a 0110 (clase de los elementos) la negamos, obtenemos su opuesto: 1001. Sus constituyentes no desaparecen, solo cambian de lugar. Si volvemos a negar, obtenemos (según la lógica clásica) la estructura inicial. Se establece así, una dinámica cíclica que podría caracterizarse como la tendencia de ir hacia el objeto (10) a través del sujeto (01). Esta dinámica se puede asimilar a una función (una estructura proyectada en otra estructura) que llamaremos: organización y que representa una transformación o cambio evidente y no significa otra cosa que la disyunción entre ambos polos de la relación (11 = V). Ahora, si negamos 01(S), no desaparece pasando a 10(O), sino que ‘pasa’ a 11(V); y si esta última se niega, ‘pasa’ a 10(O). Luego, 11(V) se transforma en una clase mediadora entre los polos opuestos y cambia entonces, el concepto de negación. Es como si se negara los continentes o nichos y no el contenido, y de esta forma, hay un ‘desplazamiento conservador’ ( Hegel) de un extremo a otro obtenido por la ‘negación de la negación (Hegel). Alcanzado 10(O); si se vuelve a negar, se obtiene 00(⊽), lo cual significa otra transformación o cambio (en este caso oculto) que representa ahora, la conjunción de los extremos la que llamaremos desorganización. Si negásemos 00(⊽) llegaríamos a 01(S), completándose un ciclo reflexivo (Hegel). En realidad, son dos ciclos completos ‘ensamblados’ que ‘giran’ en sentido opuesto (el tercer infinito) (figura 3).
El ensamble definido recibe como nombre PAU (Patrón Autónomo Universal) y es considerado aquí, como la unidad de complejidad real. Queda constituido un verdadero sistema como manifestación concreta de la mínima expresión de realidad que se pueda concebir. Su complejidad reside en que las dos ‘triadas’ que lo componen: SVO y O⊽S, están ligadas por una triple relación: i) son opuestas, O⊽S (100001) es la negación de SVO (011110); ii) son complementarias, cada una tiene, a su vez, una característica de la que la otra carece y viceversa ; y iii) son simultáneas o concurrentes, se producen al mismo tiempo. Por otro lado, son complementarias bajo dos aspectos: a) en el ya mencionado, y b) en el que surge dado su ‘sentido de giro’.
Finalmente podemos decir que a este sistema lo animan dos lógicas: una superficial y binaria, ya que ‘gira a saltos’; por ‘pares’ de elementos y que se encarga de que el sistema, en su apariencia, ‘encaje’ en la lógica formal; y una profunda y continua, con infinitos valores intermedios entre 1 y 0, a la cual le llamamos difusa o borrosa. Todo el sistema a su vez, está regido por una única lógica polivalente (tetravalente, cuyos valores de verdad no son 1 y 0 como en la lógica binaria, sino 00, 01, 10 y 11), que da la posibilidad de representar el devenir de los hechos o procesos reales (en cualquier nivel que se considere la realidad), razón por la cual la llamaremos Lógica Transcursiva o del transcurrir.
La Lógica Transcursiva, por el hecho de servir para representar integralmente la realidad, de acuerdo a lo aquí propuesto, también es apta para representar cualquier manifestación psíquica, biológica y lingüístico-social que se supone representan distintos aspectos de un universo determinado (sea éste concreto o virtual).
Borges, desde su sapiencia nos muestra, que lo finito (discreto y aparente) y lo infinito (continuo y oculto) pueden coexistir, aunque la lógica tradicional (convencional) no lo admita, y que la apariencia (esa gran ‘mentirosa’) regodeándose en sus límites, deja escapar algunas ‘pistas’ como las del espejo (algo de lo que ‘pocos’ se percataron), que sirven para mantener la esperanza de una infinitud que en apariencia nunca alcanzaremos.
La realidad borgeana es la de su biblioteca, la de su universo; la de ‘nuestro’ universo y por ende, la de nuestra vida; esa realidad que nunca será atrapada en un algoritmo por complejo que éste sea, ni se dejará encasillar en axiomas por más ‘lógicos’ que parezcan.
A través de la semiosis, concebida como una acción reorganizadora de un sistema lógico, hemos visto que es posible, como también nos lo mostró Borges, abordar la realidad, allende de la lógica tradicional, por alternativas que le pueden asignar así mismo, un sentido.
¡Nos vemos mañana!
(El 23/7/2008 se publica en Aprend3r la segunda parte de "Ficciones", y es lo que hoy veremos en este capítulo)
Ficciones (Segunda Parte)
En esta segunda parte intentaremos caracterizar una observación semiótica de la realidad, considerando la Semiótica como la lógica del sentido (según ya vimos). El hecho de basarse en la observación como método de análisis es adecuado, ya que de esta forma se evita la ‘presunción imperialista’ (como dice Eco) de suponer que la Semiótica puede explicarlo todo. Todo puede ser tratado semióticamente, que es algo muy distinto.
Para comenzar debemos establecer parámetros concretos, reales y tangibles para poder así procurar una definición (aproximarse al límite aristotélico) de algunos conceptos que por ser tales, carecen (en apariencia ) de realidad. Uno, entre otros, que necesita imperiosamente de un límite es el concepto de infinito (qué paradójico, ¿No?).
Hemos dicho que no hay nada infinito. Esto, a primera vista, es cierto si nos referimos a la apariencia que nos ofrecen los cuerpos materiales; pero, no lo es tanto si pretendemos justificar otras cosas. Entonces nos percatamos que pueden definirse, al menos, tres infinitos: a) Un infinito por suma, que es el concepto de Número; b) Un infinito por división, que es el concepto de Espacio; y c) Un infinito en ambos sentidos, que es el concepto de Tiempo. Luego, tendría sentido presuponer una infinitud corpórea que ha de entenderse como lo contrario a evidente, superficial y discreto. Este es un infinito que se alcanzaría paulatinamente, en forma oculta, en ‘las profundidades’ de la realidad, y, que surgiría explosivamente a la apariencia (se manifestaría como ‘verdad’) en un ir haciéndose; en un alcanzar el límite; en un provocar catástrofes; en un producir bifurcaciones; en una palabra, en un definirse. Esta definición lo es a modo de una perturbación variable (cambio) aunque con cierta estabilidad que en cada instante del tiempo irreversible tiene dimensiones finitas, a pesar de manifestarse por un Número y ocupar un Espacio en un Tiempo determinado, que no lo son.
Habiendo de alguna manera, ‘corporeizado’ el infinito, retomamos la Babel borgeana, en la que, más allá de los múltiples acertijos (de los que haremos caso omiso) hay un fuerte planteo paradojal, dialéctico (en el sentido hegeliano; o mejor heracliteano) y según trataremos de demostrar, real.
Ya desde Einstein quedó claramente establecido (muy a pesar de Newton), que toda simultaneidad es relativa. Esta relatividad tiene que ver con el simple hecho de estar obligados a elegir un sistema de referencia particular (no olvidar que en ciencia trabajamos con convenciones). Borges nos plantea algo distinto al absoluto newtoniano y al relativismo de Einstein; aproximándose a los presocráticos, nos pinta un universo cual pergeño alucinante de un devenir perpetuo de polos opuestos simultáneos que en su cíclico cambio, siempre termina (para comenzar) siendo lo mismo.
Todo esto suena a ilógico, a meros términos ‘sin sentido’, a un ruido de fondo que intenta tapar la evidencia; a un protocolo aventurado que nunca conseguirá ponerse a la altura de las circunstancias formales y por más que de ‘vueltas’, nunca será más que un delirante paralogismo. Si lo vemos con los ojos de la lógica clásica, sí. Si corregimos nuestra miopía con la óptica de una de las tantas lógicas alternativas posibles, no.
Imaginemos solo por un instante, que nos hemos propuesto descifrar la estructura de la realidad (¡Menuda tarea!)
Si hablamos de estructura, hablamos de relaciones; y si hablamos de relaciones, estamos diciendo algo sobre elementos que se relacionan; y si hablamos de elementos, estamos resaltando diferencias y además la simultaneidad en la aprehensión de al menos dos elementos distintos.
La concurrencia de la aprehensión de dos elementos exige, por un lado, que ambos tengan algo en común y por otro, que haya algo que los diferencie. Veamos esto último a través de un ejemplo simple: supongamos que tenemos ante nosotros dos pelotas, y que una de ellas es rayada y la otra lisa. Estos elementos están relacionados de dos maneras en forma simultánea: tienen algo en común que los identifica como pelota (p.e. la forma) y algo que los diferencia como elementos distintos pertenecientes a una categoría determinada, el hecho de ser una rayada, y la otra no.
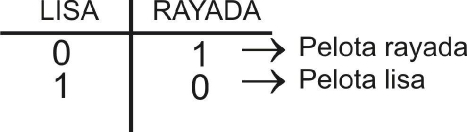
Tabla I
La tabla I muestra una manera (entre otras) de representar ‘numéricamente’ ambas pelotas (que ya es ‘rozar’ uno de los infinitos). Este método se basa en dejar constancia de las oposiciones que caracterizan los elementos; o sea, de aquello que permite distinguirlos (presencia o ausencia de un atributo dado).
Se puede observar que la cifra que representa cada elemento, tiene dos lugares, entonces, la mitad no ocupada (representada por el 0), se la asignaremos a aquel atributo que hace que los dos elementos pertenezcan a la misma categoría (la forma); es decir, para consignar que ambos son pelotas. Esta simple estructura se puede representar como lo muestra la (figura 1).
Figura 1
Desde el punto de vista lógico podemos ver, en la Figura 1, que ambos elementos guardan una doble relación: i) son opuestos; es decir, uno es la negación del otro (negar 01 es reemplazarlo por su inverso 10, y viceversa), y ii) son complementarios porque uno tiene una característica de la que el otro carece. Pero además este esquema nos muestra otros aspectos relacionales que subyacen a la aprehensión de ambos elementos. Así, por un lado tenemos la conjunción por aquel aspecto o atributo que tienen en común (la forma), y por otro la disyunción por aquel atributo que los diferencia (textura).
La conjunción como operación lógica nos dice que una relación será verdadera (y asumirá un valor 1) cuando ambos elementos de la relación sean verdaderos (evidentes), de lo contrario será falsa (asumirá un valor 0); por eso 01∩10 = 00. En cuanto a la disyunción nos dice que será falsa (0) únicamente cuando ambos elementos disyuntivos sean falsos, de lo contrario será verdadera (1); entonces 01∪10 = 11.
De acuerdo a lo anterior estamos autorizados para decir, según la lógica de clases, que 11 representa la unión de aquellos aspectos que distinguen un elemento de otro, y que 00 representa la separación (intersección) de aquel aspecto que los reúne (categoría). Es importante notar además, que 11 y 00 guardan entre sí la misma doble relación de oposición y complementariedad. Por tanto, y siguiendo en la lógica de clases, podemos afirmar que en este pequeño universo que hemos caracterizado, hay dos clases o conjuntos: la de los elementos (con su ámbito (01) y su complemento (10)), y la del cambio o transformación (con su ámbito (11) y su complemento (00)) que surge cuando dos objetos se relacionan entre sí.
Cuando analizamos otras oposiciones relacionadas con los mismos objetos, descubrimos algo interesante. Por ejemplo, pelota grande vs. pelota pequeña. Esta última oposición ya no es binaria (no tiene solo dos términos: el elemento y su opuesto), sino que al menos, admite un término intermedio como lo es pelota mediana. En realidad este tipo de atributos, acepta infinitos valores entre sus extremos. De esta manera, si pretendemos ‘describir’ lo que ocurre en la realidad de este nuestro limitado universo, debemos poder caracterizar todas las posibilidades. Una forma de hacerlo es ampliar el esquema anterior, profundizando en su estructura y mostrar así, que en definitiva, todo se restringe a un interjuego entre el ‘ser’ y el ‘parecer’. El ‘parecer’, aquello que se ofrece en directo a la aprehensión y que tildaremos de ‘superficial’, es de tipo binario o discreto; se pasa de un extremo al otro de la comparación sin valores intermedios, siendo así un atributo absoluto y evidente. El ‘ser’ en cambio, es aquello que ‘no se ve’, que permanece oculto y por lo que lo llamamos profundo y admite infinitos valores intermedios entre sus extremos; esta última característica lo convierte en un atributo continuo o analógico y relativo pues resulta su valoración, de una comparación (de un marco de referencia).
Hipotéticamente y de una forma genérica, se puede utilizar como base de la observación semiótica la relación sujeto/objeto. Aquí sujeto (S) es considerado como la ‘fuente’ del cambio y el objeto (O) como el ‘destino’ de ese cambio, y ambos están relacionados precisamente por tal cambio que queda expresado por una operación de disyunción (cambio aparente = V) en la superficie y por una operación de conjunción (cambio oculto = ⊽) en lo profundo. (figura 2)
Figura 2
Los vértices del ‘cuadrado’ propuesto (figura 2) representan lo que llamamos: nichos o lugares ontológicos, que serán ocupados por elementos de sentido (contenidos) concretos (el segundo infinito); contenidos que, en la elaboración de la dinámica, no son tenidos en cuenta.
Si a 0110 (clase de los elementos) la negamos, obtenemos su opuesto: 1001. Sus constituyentes no desaparecen, solo cambian de lugar. Si volvemos a negar, obtenemos (según la lógica clásica) la estructura inicial. Se establece así, una dinámica cíclica que podría caracterizarse como la tendencia de ir hacia el objeto (10) a través del sujeto (01). Esta dinámica se puede asimilar a una función (una estructura proyectada en otra estructura) que llamaremos: organización y que representa una transformación o cambio evidente y no significa otra cosa que la disyunción entre ambos polos de la relación (11 = V). Ahora, si negamos 01(S), no desaparece pasando a 10(O), sino que ‘pasa’ a 11(V); y si esta última se niega, ‘pasa’ a 10(O). Luego, 11(V) se transforma en una clase mediadora entre los polos opuestos y cambia entonces, el concepto de negación. Es como si se negara los continentes o nichos y no el contenido, y de esta forma, hay un ‘desplazamiento conservador’ ( Hegel) de un extremo a otro obtenido por la ‘negación de la negación (Hegel). Alcanzado 10(O); si se vuelve a negar, se obtiene 00(⊽), lo cual significa otra transformación o cambio (en este caso oculto) que representa ahora, la conjunción de los extremos la que llamaremos desorganización. Si negásemos 00(⊽) llegaríamos a 01(S), completándose un ciclo reflexivo (Hegel). En realidad, son dos ciclos completos ‘ensamblados’ que ‘giran’ en sentido opuesto (el tercer infinito) (figura 3).
Figura 3
El ensamble definido recibe como nombre PAU (Patrón Autónomo Universal) y es considerado aquí, como la unidad de complejidad real. Queda constituido un verdadero sistema como manifestación concreta de la mínima expresión de realidad que se pueda concebir. Su complejidad reside en que las dos ‘triadas’ que lo componen: SVO y O⊽S, están ligadas por una triple relación: i) son opuestas, O⊽S (100001) es la negación de SVO (011110); ii) son complementarias, cada una tiene, a su vez, una característica de la que la otra carece y viceversa ; y iii) son simultáneas o concurrentes, se producen al mismo tiempo. Por otro lado, son complementarias bajo dos aspectos: a) en el ya mencionado, y b) en el que surge dado su ‘sentido de giro’.
Finalmente podemos decir que a este sistema lo animan dos lógicas: una superficial y binaria, ya que ‘gira a saltos’; por ‘pares’ de elementos y que se encarga de que el sistema, en su apariencia, ‘encaje’ en la lógica formal; y una profunda y continua, con infinitos valores intermedios entre 1 y 0, a la cual le llamamos difusa o borrosa. Todo el sistema a su vez, está regido por una única lógica polivalente (tetravalente, cuyos valores de verdad no son 1 y 0 como en la lógica binaria, sino 00, 01, 10 y 11), que da la posibilidad de representar el devenir de los hechos o procesos reales (en cualquier nivel que se considere la realidad), razón por la cual la llamaremos Lógica Transcursiva o del transcurrir.
La Lógica Transcursiva, por el hecho de servir para representar integralmente la realidad, de acuerdo a lo aquí propuesto, también es apta para representar cualquier manifestación psíquica, biológica y lingüístico-social que se supone representan distintos aspectos de un universo determinado (sea éste concreto o virtual).
Borges, desde su sapiencia nos muestra, que lo finito (discreto y aparente) y lo infinito (continuo y oculto) pueden coexistir, aunque la lógica tradicional (convencional) no lo admita, y que la apariencia (esa gran ‘mentirosa’) regodeándose en sus límites, deja escapar algunas ‘pistas’ como las del espejo (algo de lo que ‘pocos’ se percataron), que sirven para mantener la esperanza de una infinitud que en apariencia nunca alcanzaremos.
La realidad borgeana es la de su biblioteca, la de su universo; la de ‘nuestro’ universo y por ende, la de nuestra vida; esa realidad que nunca será atrapada en un algoritmo por complejo que éste sea, ni se dejará encasillar en axiomas por más ‘lógicos’ que parezcan.
A través de la semiosis, concebida como una acción reorganizadora de un sistema lógico, hemos visto que es posible, como también nos lo mostró Borges, abordar la realidad, allende de la lógica tradicional, por alternativas que le pueden asignar así mismo, un sentido.
¡Nos vemos mañana!