Historia de la Lógica Transcursiva (Capítulo 133)
Cuaderno VI (páginas 795 a 800)
(Continuamos con el abordaje de la realidad que hace la Lógica Difusa)
- Variables lingüísticas: son aquellos conceptos o nociones que se califica de forma difusa, para dar cuenta de su carácter continuo (altura, edad, nivel emocional, etc.). Se denominan 'lingüísticos' porque se definen mediante términos del lenguaje común.
-Valor lingüístico: los distintas calificaciones que efectúan sobre la variable lingüística: muy joven, algo joven, poco joven, no joven, etc. (joven, maduro, viejo).
Al conjunto difuso (CD) ahora lo podemos definir como un valor lingüístico junto a una función de pertenencia. El valor es el 'nombre' del conjunto y la función de pertenencia es aquella aplicación que asocia a cada elemento del universo, el grado con que pertenece al CD, indicando su relación con cada valor lingüístico.
Se dice que un conjunto es 'nítido' si su función de pertenencia toma valores {0,1} y 'difuso' si toma valores entre [0,1]. (figura)
Otras definiciones útiles sobre los CD:
- Soporte: de un CD A es el conjunto nítido de elementos que tienen grado de pertenencia estrictamente mayor a 0.
Soporte(A) = {x∈X/μA(x) > 0}
- Núcleo: de un CD A es el conjunto nítido de elementos que tienen grado de pertenencia = 1.
Núcleo(A) = {x∈X/μA(x) > 1}
- Altura: de un CD A es el valor más grande de su función de pertenencia
Se dice que un CD está normalizado, si y solo si, su núcleo contiene algún elemento, o alternativamente, si su altura es 1.
∃x/x∈X o μA(x) = 1 ∈ = pertenece / ∃x = existe al menos un x tal que ...
El elemento x de X para el cual μA(x) = 0,5 se llama 'punto de cruce'
Un CD cuyo soporte es un único punto x de X, tal que la función de pertenencia de x es 1, o sea, el soporte coincide con el núcleo y tiene un único punto, se llama CD unitario (singletón).
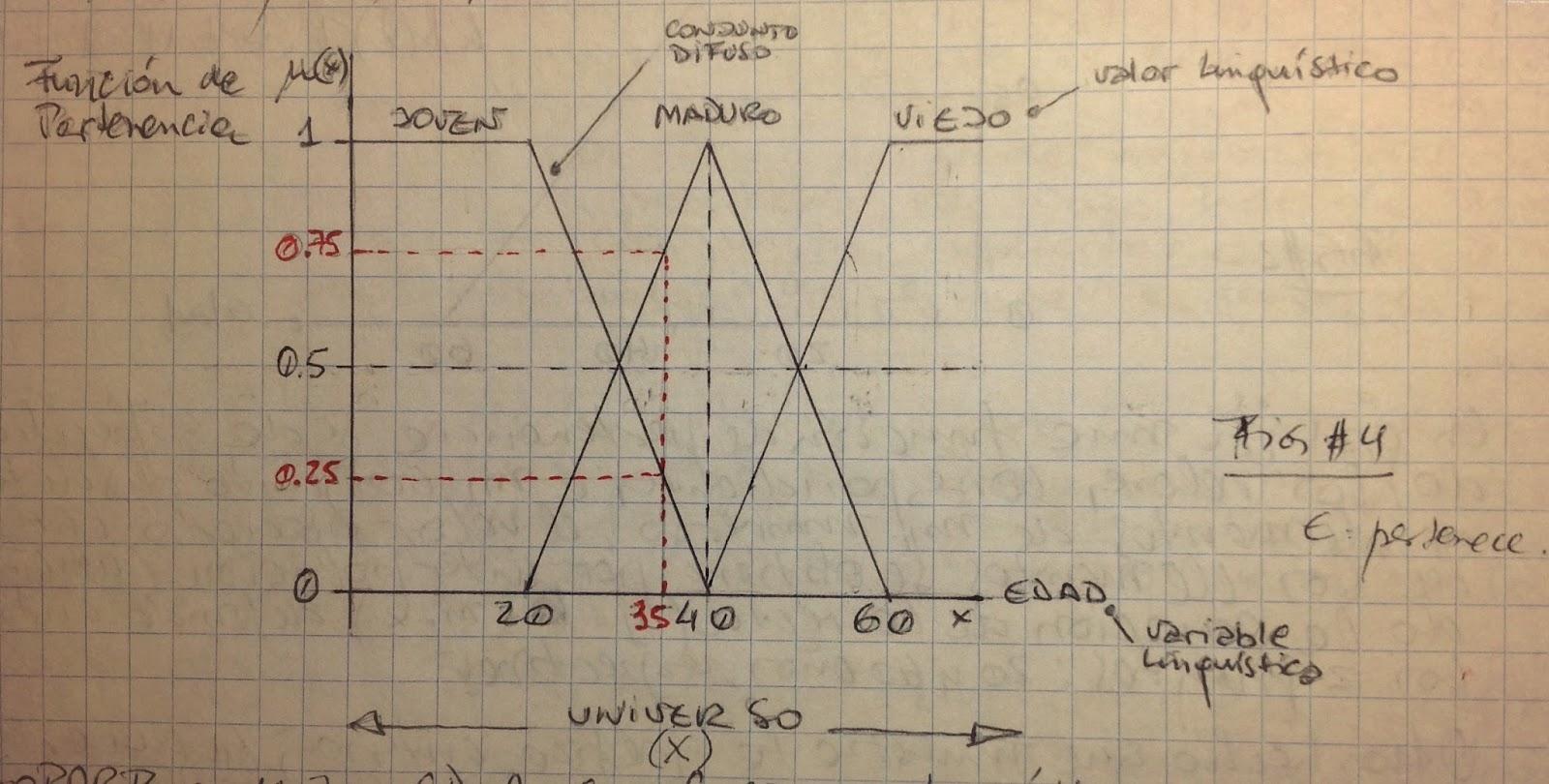
Para el CD 'maduro' de la figura anterior tenemos:
soporte = (20, 60)
núcleo = 40
Es un CD normalizado y tiene dos puntos de cruce: 30 y 50.
También son permite ver que una persona de 35 años es 25% joven y 75% maduro.
¿Cómo se puede calcular esto? (figura siguiente).
A través de la función de pertenencia, que dada su forma gráfica recibe distintos nombres y tiene un cálculo particular que se basa en el mismo principio utilizado en el gráfico del capítulo anterior en donde se calculaba el ºG de juventud.
Otras funciones de pertenencia:
Las funciones L y Gamma, de la figura anterior, se usan para calificar valores lingüísticos extremos, como joven o viejo; y las funciones PI (trapezoidal de la figura adjunta) y Lambda (triangular) para valores intermedios, como por ejemplo: maduro. La principal diferencia es que PI tiene un margen de tolerancia alrededor del falos tomado como más representativo del valor lingüístico asociado al CD.
Se pueden utilizar otras funciones que no sean líneas quebradas, sino una línea continual. (figura siguiente)
Tradicionalmente se utilizan modificadores de los CD que en el lenguaje natural serían los 'adverbios'; sin entrar en detalles se listan, a continuación, algunos de los más utilizados:
Por ejemplo: si μ(x) de una persona al CD de los 'altos' es 0,5, la de μ(x) al CD 'muy altos' es de (0,5)² = 0,25.
- Operaciones elementales con CDs.:
- Complemento: dado un conjunto A, el conjunto complementario de A contiene todos los elementos del universo que no pertenecen (∉) a A y se representa como A⃩. En el caso difuso generalmente se define como A⃩(x) = 1 - A(x).
Ley del complemento:
A + (-A) = 1
A . (-A) = 0 En el caso del CD 'maduro' sería: (figura siguiente)
Las funciones verdaderamente difusas definen un conjunto de operaciones difusas, como un conjunto de funciones: supongamos que X es un espacio base que contiene los subconjuntos difusos A y B, luego:
a⃩(x) = 1 - a(x)
a(x)∩b(x) = min(a(x), b(x)) ∩ = intersección (.)
a(x)∪b(x) = max(a(x), b(x)) ∪ = unión (+)
- Conjunto intersección (CI)(∩): un elemento ∈ a un CI de dos conjuntos si ∈ a ambos (solapamiento o superposición) {también producto lógico}.
- Conjunto unión (CU)(∪): un conjunto unión de dos conjuntos tiene todos los elementos de ambos conjuntos. (figura)
Un conjunto A⊂X (⊂ = es subconjunto de) es difuso, si y solo si, rompe el principio de no contradicción: A∩A ≠ 0, y el principio del tercero excluido: A∪A ≠ X. Un conjunto es bivalente (o nítido) si la igualdad se da en ambos conjuntos de relaciones (A∩A = 0; A∪A⃩ = X).
Un CD tiene varias formas, en varios contextos. Ya vimos que un CD puede ser un concepto 'vago' o de límites borrosos. Puede ser un objeto abstracto como los 'números cercanos a 10', que parcialmente contiene otros objetos. Un CD también puede ser un subconjunto vago de un espacio como: 'grandes montañas en la cordillera de Los Andes', o el conjunto de 'muestras aleatorias estadísticamente significativas, en un espacio de muestreo'. Puede ser una función que 'busque objetos' en un espacian de los números entre 0 y 1. Esta última opción es una vista algebraica o como función de un CD.
Un CD en fin, puede ser un 'punto' en algún espacio. Esta es la vista geométrica de un CD {de gran interés para nuestros propósitos}, o la vista de conjuntos como puntos. Un CD tipo triángulo o campana, como el de personas maduras que hemos visto, define un punto en un espacio-función abstracto de un conjunto de funciones. Estos espacios no pueden 'verse' en la realidad pero existen (como ya veremos). Si bien no se pueden 'ver' sí se puede comprender la 'distancia' entre dos CDs., como el 'largo' de un segmento de línea que conecta dos puntos, o como la vecindad de un CD como una esfera que contiene un CD como un punto en su centro, o un CD cambiante o adaptativo como un punto moviéndose a través del espacio.
Un CD discreto tiene una geometría simple; él es un punto en un cubo difuso. Un cubo difuso es un hipercubo unidad que tiene el intervalo unidad [0,1] como cada uno de sus lados. El intervalo unidad forma, por sí mismo, el más simple de los hipercubos difusos o cubo 1D y que aloja un objeto y con él, todos los valores verdaderos de una lógica difusa o multivaluada. (parte alta, figura siguiente)
Aquí, un objeto puede variar desde 100% presente a 0% presente {o 100% ausente}.
Una unidad cuadrada (parte baja, figura adjunta) aloja todos los subconjuntos difusos de 2 objetos.
La unidad cubo aloja todos los subconjuntos de 3 objetos (figura siguiente), y así sucesivamente hasta el infinito.
Todos los 'hipercubos' tienen un único punto medio o que es equidistante de sus 'esquinas binarias'.
Para representar estos conjuntos de objetos (que en rigor son conjuntos finitos parcialmente ordenados) se utilizan estos 'grafos dirigidos' que proporcionan una representación gráfica del orden definido en el conjunto (diagrama de Hasse), y en donde el número de 'vértices' está definido por 2ⁿ (n = cantidad de objetos). Así: 2⁰ = 1(un punto); 2¹ = 2(cubo 1D = línea); 2² = 4(cubo 2D = plano); 2³ = 8(cubo 3D = cubo); etc.
Los conjuntos no difusos descansan en los 'vértices' del hipercubo. Es allí y solo allí donde ellos 'obedecen' las leyes de la lógica bivalente. [la Teoría final demostrará que esto no es correcto.] Las diagonales largas conectan un conjunto bivalente co su opuesto o complementario. Estas diagonales largas deben pasar por el punto medio del cubo. [las dos figuras anteriores] El operador NOT (negación) hace que los extremos bivalentes opuestos 'salten' sobre el punto medio para pasar de A a no A (A⃩).
Los CDs. rellenan el cubo. Ellos se hacen 'difusos' a medida que se aproximan al punto medio único del cubo. El conjunto 'punto medio' es el más difuso de todos porque tiene 'parte' iguales de sus oponentes (simultaneidad o co-presencia). Un cubo difuso contiene todos los subconjuntos difusos de un conjunto X de n objetos. Los 2ⁿ vértices del n-cubo [0,1]ⁿ. El continnum de los CDs, rellena el cubo. Estos cubos son 'biológicos': bivalentes por sus extremos y difusos por su centro.
Para mostrar las relaciones que ligan las distintas operaciones básicas entre los CD que hemos bosquejados, veremos un ejemplo sencillo. Supongamos la siguiente situación: (figura siguiente)
Como se consideran dos objetos (2² = 4) se definen 4 vértices.
El punto A (¼, ⅔) define un subconjunto difuso de 2 objetos (x1, x2).
Este tiene el subconjunto difuso complementario
A⃩ = (¾, ⅓).
Estos dos puntos están en los vértices de un 'cuadrado interior' con un vértice definido por la intersección A∩A⃩(¼, ⅓), y el otro por la unión
A∪A⃩(¾, ⅔). Las diagonales mayores conectan ambos pares de puntos complementarios.
Los 4 puntos difusos se 'contraen' hacia el punto medio en la medida que A se hace más difuso, y se 'expanden' hacia los vértices binarios en la medida que A se hace más nítido. {y todos los objetos nítidos que a su vez son complementarios}
Entonces: (figura siguiente)
El ejemplo anterior deja más claro aún que el punto medio del cubo, cuando A descansa en el punto medio de ambos objetos es donde la mayoría de A parece A⃩(no A), rompiendo con los principios de no contradicción y del tercero excluido de la lógica aristotélica. [lo cual no es cierto como más adelante se demostrará] Este punto medio es el conjunto más difuso de todos y solo él obedece la relación 'paradójica': A = A⃩ [lo cual no tiene ningún sentido, como no sea para 'simular' el no respeto de la lógica de Aristóteles. A y A⃩, para la LT son opuestos, complementarios y concurrentes, pero jamás iguales.] No hay manera binaria de precisar este punto medio de un cubo [lo cual también constituye un error que, intencionadamente no es señalado. En lo único sentido que A = A⃩ es en que ambos, en el punto medio, tienen 50% de 'presencia', pero eso no los hace iguales, al contrario, nunca han sido más opuestos que en este punto medio.] de uno de los 2ⁿ vértices binarios. A∪A⃩ están contenidos en el 100% de los vértices del cubo (conjuntos binarios o nítidos u objetos). A∩A⃩ están contenidos en el punto medio del cubo. [estas dos últimas afirmaciones son absolutamente correctas, por tanto, contradicen totalmente toda la argumentación anterior. En pocas palabras: A ≠ A⃩.]
Esto tiene la trascendencia de demostrar que la 'paradoja' en la lógica, de alguna manera, es la regla y no la excepción. [afirmación que es una falacia.]
Hasta aquí podemos decir que hemos podido caracterizar los dos extremos de lo real, a saber: por un lado, lo nítido, lo discreto, lo determinable; los objetos (mediante la lógica bivalente); y por otro lado, lo borroso, lo continuo, lo incierto (mediante la lógica difusa); e inclusive, hemos visto la posibilidad de ir de un extremo a otro.
No obstante ello, hay un gran abismo entre lo discreto y lo continuo; siguen apareciendo como 'extremos' [irreconciliables], como opuestos y solo eso. Es más que obvio que la realidad, y por ende, sus sistemas constitutivos muestran una marcada dinámica, que justamente, caracteriza la gran variabilidad real.
Hay dos factores que deben ser tenidos en cuenta, como fundamento, para poder caracterizar lógicamente a los sistemas reales, fuera de la existencia de 'opuestos', y ellos son: la simultaneidad o concurrencia de los extremos y la 'ligadura' entre ellos.
Comenzaremos por el último y para ello vamos a proponer como soporte, la lógica relacional. Si bien la lógica de las relaciones es un amplio capítulo de la lógica simbólica, aquí solo nos interesaremos por dos aspectos: las relaciones de orden y las relaciones entre relaciones. [aquí, en este segundo aspecto tendrá lugar la irrupción de la lógica transclásica de Günther]
Como en los casos anteriores, daremos algunas definiciones básicas estrictamente necesarias para manejarnos en nuestro planteo. Para precisar el concepto de 'relación' es necesario definir un 'par ordenado', y en general, lo que se llama 'n-tupla'. Un par ordenado o dupla es un par de elementos que se dan en un orden determinado: uno primero (x) y otro después (y): <x, y>.
En las clases lógicas o categorías este orden es irrelevante, sin embargo, en las clases o categorías reales [esta nomenclatura luego será abandonada y reemplazada por 'especies'.] veremos que no lo es. Cuando en vez de 2, 3 son los elementos dados en cierto orden, se los denomina tripla <x, y, z>; si son 4: cuádrupla; y en general: n-tupla.
De acuerdo a lo anterior, la clase de relaciones cuyos miembros son duplas, se dice que tiene un 'grado 2' y se la llama relación diádica; la que tiene triplas posee un grado 3 y se la llama triádica; en general, a la de grado n, n-ádica.
Al elemento primero, el que inicia la relación en una dupla, por ejemplo, se lo denomina: 'referente'. Nos tomamos la licencia de considerarlo como 'fuente' de una determinada relación. Al segundo elemento de una dupla se lo denomina 'relato'; nosotros lo consideramos como 'destino' de esta relación. Esta distinción es estrictamente 'sintáctica' (relaciones entre símbolos), o sea que tiene que ver con el aspecto estructural de la realidad (el qué), y por tanto, caracteriza a los actores necesarios de los sistemas reales (S, O) como luego veremos.
¡Nos vemos mañana!
(Continuamos con el abordaje de la realidad que hace la Lógica Difusa)
- Variables lingüísticas: son aquellos conceptos o nociones que se califica de forma difusa, para dar cuenta de su carácter continuo (altura, edad, nivel emocional, etc.). Se denominan 'lingüísticos' porque se definen mediante términos del lenguaje común.
-Valor lingüístico: los distintas calificaciones que efectúan sobre la variable lingüística: muy joven, algo joven, poco joven, no joven, etc. (joven, maduro, viejo).
Al conjunto difuso (CD) ahora lo podemos definir como un valor lingüístico junto a una función de pertenencia. El valor es el 'nombre' del conjunto y la función de pertenencia es aquella aplicación que asocia a cada elemento del universo, el grado con que pertenece al CD, indicando su relación con cada valor lingüístico.
Se dice que un conjunto es 'nítido' si su función de pertenencia toma valores {0,1} y 'difuso' si toma valores entre [0,1]. (figura)
Otras definiciones útiles sobre los CD:
- Soporte: de un CD A es el conjunto nítido de elementos que tienen grado de pertenencia estrictamente mayor a 0.
Soporte(A) = {x∈X/μA(x) > 0}
- Núcleo: de un CD A es el conjunto nítido de elementos que tienen grado de pertenencia = 1.
Núcleo(A) = {x∈X/μA(x) > 1}
- Altura: de un CD A es el valor más grande de su función de pertenencia
Se dice que un CD está normalizado, si y solo si, su núcleo contiene algún elemento, o alternativamente, si su altura es 1.
∃x/x∈X o μA(x) = 1 ∈ = pertenece / ∃x = existe al menos un x tal que ...
El elemento x de X para el cual μA(x) = 0,5 se llama 'punto de cruce'
Un CD cuyo soporte es un único punto x de X, tal que la función de pertenencia de x es 1, o sea, el soporte coincide con el núcleo y tiene un único punto, se llama CD unitario (singletón).
Para el CD 'maduro' de la figura anterior tenemos:
soporte = (20, 60)
núcleo = 40
Es un CD normalizado y tiene dos puntos de cruce: 30 y 50.
También son permite ver que una persona de 35 años es 25% joven y 75% maduro.
¿Cómo se puede calcular esto? (figura siguiente).
A través de la función de pertenencia, que dada su forma gráfica recibe distintos nombres y tiene un cálculo particular que se basa en el mismo principio utilizado en el gráfico del capítulo anterior en donde se calculaba el ºG de juventud.
Otras funciones de pertenencia:
Se pueden utilizar otras funciones que no sean líneas quebradas, sino una línea continual. (figura siguiente)
Tradicionalmente se utilizan modificadores de los CD que en el lenguaje natural serían los 'adverbios'; sin entrar en detalles se listan, a continuación, algunos de los más utilizados:
Por ejemplo: si μ(x) de una persona al CD de los 'altos' es 0,5, la de μ(x) al CD 'muy altos' es de (0,5)² = 0,25.
- Operaciones elementales con CDs.:
- Complemento: dado un conjunto A, el conjunto complementario de A contiene todos los elementos del universo que no pertenecen (∉) a A y se representa como A⃩. En el caso difuso generalmente se define como A⃩(x) = 1 - A(x).
Ley del complemento:
A + (-A) = 1
A . (-A) = 0 En el caso del CD 'maduro' sería: (figura siguiente)
a⃩(x) = 1 - a(x)
a(x)∩b(x) = min(a(x), b(x)) ∩ = intersección (.)
a(x)∪b(x) = max(a(x), b(x)) ∪ = unión (+)
- Conjunto intersección (CI)(∩): un elemento ∈ a un CI de dos conjuntos si ∈ a ambos (solapamiento o superposición) {también producto lógico}.
- Conjunto unión (CU)(∪): un conjunto unión de dos conjuntos tiene todos los elementos de ambos conjuntos. (figura)
Un conjunto A⊂X (⊂ = es subconjunto de) es difuso, si y solo si, rompe el principio de no contradicción: A∩A ≠ 0, y el principio del tercero excluido: A∪A ≠ X. Un conjunto es bivalente (o nítido) si la igualdad se da en ambos conjuntos de relaciones (A∩A = 0; A∪A⃩ = X).
Un CD tiene varias formas, en varios contextos. Ya vimos que un CD puede ser un concepto 'vago' o de límites borrosos. Puede ser un objeto abstracto como los 'números cercanos a 10', que parcialmente contiene otros objetos. Un CD también puede ser un subconjunto vago de un espacio como: 'grandes montañas en la cordillera de Los Andes', o el conjunto de 'muestras aleatorias estadísticamente significativas, en un espacio de muestreo'. Puede ser una función que 'busque objetos' en un espacian de los números entre 0 y 1. Esta última opción es una vista algebraica o como función de un CD.
Un CD en fin, puede ser un 'punto' en algún espacio. Esta es la vista geométrica de un CD {de gran interés para nuestros propósitos}, o la vista de conjuntos como puntos. Un CD tipo triángulo o campana, como el de personas maduras que hemos visto, define un punto en un espacio-función abstracto de un conjunto de funciones. Estos espacios no pueden 'verse' en la realidad pero existen (como ya veremos). Si bien no se pueden 'ver' sí se puede comprender la 'distancia' entre dos CDs., como el 'largo' de un segmento de línea que conecta dos puntos, o como la vecindad de un CD como una esfera que contiene un CD como un punto en su centro, o un CD cambiante o adaptativo como un punto moviéndose a través del espacio.
Un CD discreto tiene una geometría simple; él es un punto en un cubo difuso. Un cubo difuso es un hipercubo unidad que tiene el intervalo unidad [0,1] como cada uno de sus lados. El intervalo unidad forma, por sí mismo, el más simple de los hipercubos difusos o cubo 1D y que aloja un objeto y con él, todos los valores verdaderos de una lógica difusa o multivaluada. (parte alta, figura siguiente)
Una unidad cuadrada (parte baja, figura adjunta) aloja todos los subconjuntos difusos de 2 objetos.
La unidad cubo aloja todos los subconjuntos de 3 objetos (figura siguiente), y así sucesivamente hasta el infinito.
Para representar estos conjuntos de objetos (que en rigor son conjuntos finitos parcialmente ordenados) se utilizan estos 'grafos dirigidos' que proporcionan una representación gráfica del orden definido en el conjunto (diagrama de Hasse), y en donde el número de 'vértices' está definido por 2ⁿ (n = cantidad de objetos). Así: 2⁰ = 1(un punto); 2¹ = 2(cubo 1D = línea); 2² = 4(cubo 2D = plano); 2³ = 8(cubo 3D = cubo); etc.
Los conjuntos no difusos descansan en los 'vértices' del hipercubo. Es allí y solo allí donde ellos 'obedecen' las leyes de la lógica bivalente. [la Teoría final demostrará que esto no es correcto.] Las diagonales largas conectan un conjunto bivalente co su opuesto o complementario. Estas diagonales largas deben pasar por el punto medio del cubo. [las dos figuras anteriores] El operador NOT (negación) hace que los extremos bivalentes opuestos 'salten' sobre el punto medio para pasar de A a no A (A⃩).
Los CDs. rellenan el cubo. Ellos se hacen 'difusos' a medida que se aproximan al punto medio único del cubo. El conjunto 'punto medio' es el más difuso de todos porque tiene 'parte' iguales de sus oponentes (simultaneidad o co-presencia). Un cubo difuso contiene todos los subconjuntos difusos de un conjunto X de n objetos. Los 2ⁿ vértices del n-cubo [0,1]ⁿ. El continnum de los CDs, rellena el cubo. Estos cubos son 'biológicos': bivalentes por sus extremos y difusos por su centro.
Para mostrar las relaciones que ligan las distintas operaciones básicas entre los CD que hemos bosquejados, veremos un ejemplo sencillo. Supongamos la siguiente situación: (figura siguiente)
El punto A (¼, ⅔) define un subconjunto difuso de 2 objetos (x1, x2).
Este tiene el subconjunto difuso complementario
A⃩ = (¾, ⅓).
Estos dos puntos están en los vértices de un 'cuadrado interior' con un vértice definido por la intersección A∩A⃩(¼, ⅓), y el otro por la unión
A∪A⃩(¾, ⅔). Las diagonales mayores conectan ambos pares de puntos complementarios.
Los 4 puntos difusos se 'contraen' hacia el punto medio en la medida que A se hace más difuso, y se 'expanden' hacia los vértices binarios en la medida que A se hace más nítido. {y todos los objetos nítidos que a su vez son complementarios}
Entonces: (figura siguiente)
El ejemplo anterior deja más claro aún que el punto medio del cubo, cuando A descansa en el punto medio de ambos objetos es donde la mayoría de A parece A⃩(no A), rompiendo con los principios de no contradicción y del tercero excluido de la lógica aristotélica. [lo cual no es cierto como más adelante se demostrará] Este punto medio es el conjunto más difuso de todos y solo él obedece la relación 'paradójica': A = A⃩ [lo cual no tiene ningún sentido, como no sea para 'simular' el no respeto de la lógica de Aristóteles. A y A⃩, para la LT son opuestos, complementarios y concurrentes, pero jamás iguales.] No hay manera binaria de precisar este punto medio de un cubo [lo cual también constituye un error que, intencionadamente no es señalado. En lo único sentido que A = A⃩ es en que ambos, en el punto medio, tienen 50% de 'presencia', pero eso no los hace iguales, al contrario, nunca han sido más opuestos que en este punto medio.] de uno de los 2ⁿ vértices binarios. A∪A⃩ están contenidos en el 100% de los vértices del cubo (conjuntos binarios o nítidos u objetos). A∩A⃩ están contenidos en el punto medio del cubo. [estas dos últimas afirmaciones son absolutamente correctas, por tanto, contradicen totalmente toda la argumentación anterior. En pocas palabras: A ≠ A⃩.]
Esto tiene la trascendencia de demostrar que la 'paradoja' en la lógica, de alguna manera, es la regla y no la excepción. [afirmación que es una falacia.]
Hasta aquí podemos decir que hemos podido caracterizar los dos extremos de lo real, a saber: por un lado, lo nítido, lo discreto, lo determinable; los objetos (mediante la lógica bivalente); y por otro lado, lo borroso, lo continuo, lo incierto (mediante la lógica difusa); e inclusive, hemos visto la posibilidad de ir de un extremo a otro.
No obstante ello, hay un gran abismo entre lo discreto y lo continuo; siguen apareciendo como 'extremos' [irreconciliables], como opuestos y solo eso. Es más que obvio que la realidad, y por ende, sus sistemas constitutivos muestran una marcada dinámica, que justamente, caracteriza la gran variabilidad real.
Hay dos factores que deben ser tenidos en cuenta, como fundamento, para poder caracterizar lógicamente a los sistemas reales, fuera de la existencia de 'opuestos', y ellos son: la simultaneidad o concurrencia de los extremos y la 'ligadura' entre ellos.
Comenzaremos por el último y para ello vamos a proponer como soporte, la lógica relacional. Si bien la lógica de las relaciones es un amplio capítulo de la lógica simbólica, aquí solo nos interesaremos por dos aspectos: las relaciones de orden y las relaciones entre relaciones. [aquí, en este segundo aspecto tendrá lugar la irrupción de la lógica transclásica de Günther]
Como en los casos anteriores, daremos algunas definiciones básicas estrictamente necesarias para manejarnos en nuestro planteo. Para precisar el concepto de 'relación' es necesario definir un 'par ordenado', y en general, lo que se llama 'n-tupla'. Un par ordenado o dupla es un par de elementos que se dan en un orden determinado: uno primero (x) y otro después (y): <x, y>.
En las clases lógicas o categorías este orden es irrelevante, sin embargo, en las clases o categorías reales [esta nomenclatura luego será abandonada y reemplazada por 'especies'.] veremos que no lo es. Cuando en vez de 2, 3 son los elementos dados en cierto orden, se los denomina tripla <x, y, z>; si son 4: cuádrupla; y en general: n-tupla.
De acuerdo a lo anterior, la clase de relaciones cuyos miembros son duplas, se dice que tiene un 'grado 2' y se la llama relación diádica; la que tiene triplas posee un grado 3 y se la llama triádica; en general, a la de grado n, n-ádica.
Al elemento primero, el que inicia la relación en una dupla, por ejemplo, se lo denomina: 'referente'. Nos tomamos la licencia de considerarlo como 'fuente' de una determinada relación. Al segundo elemento de una dupla se lo denomina 'relato'; nosotros lo consideramos como 'destino' de esta relación. Esta distinción es estrictamente 'sintáctica' (relaciones entre símbolos), o sea que tiene que ver con el aspecto estructural de la realidad (el qué), y por tanto, caracteriza a los actores necesarios de los sistemas reales (S, O) como luego veremos.
¡Nos vemos mañana!